Wave-Wave Interactions: Wave Interference: Standing Waves

What is a Standing Wave? What causes the formation of Standing Waves?

Standing waves are produced when two waves that are traveling in opposite directions with the same amplitude and wavelength combine. In a traveling wave, the entire waveform moves in the direction of wave motion, and places where the wave was a minimum eventually become maxima as the crests and troughs pass through. In a standing wave, the maxima and nodes (where the displacement is zero) stay at the same places at all times. If one is at the node of a standing wave, the displacement there is always zero.

Experiment with this simulation to develop a more thorough understanding of standing waves. Begin by setting the same amplitude and wavenumber for the two oppositely traveling waves (blue and green plots). Press the CLAW icon to see the sum of these two waves in the bottom red plot. See what happens if you shift one wave with respect to the other by moving the phase slider. What happens if the amplitudes and/or wavenumbers arew slightly different?

The distinction between traveling and standing waves is easily seen in the mathematical represntation of these two waves, as shown below:

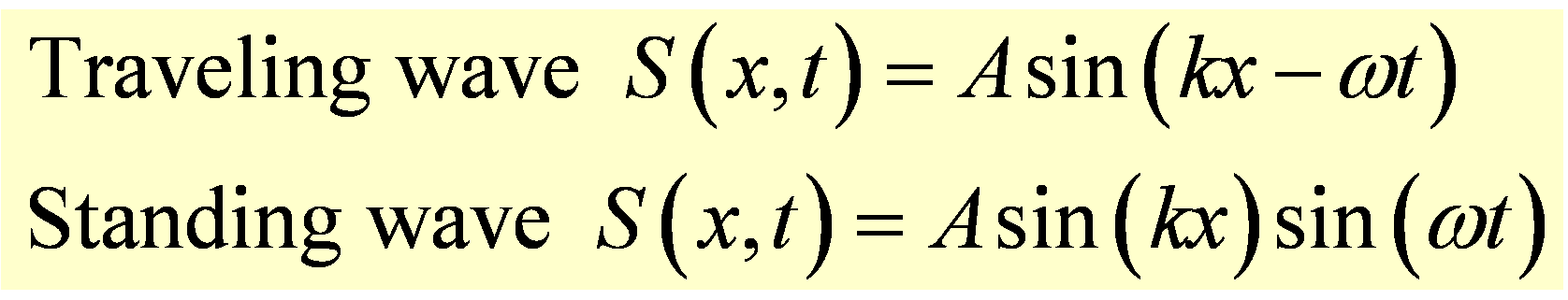
In a traveling wave, position x and time t are together inside the argument of the sine function. This argument can be kept constant as t increase by also increasing x. So to stay on the same place in the wave (argument stays the same) x must increase as t increases. If one stays at a fixed position, the displacment will oscillate sinusoidal going through full maxima and minima as time increases.

  In a standing wave, time and position are in separate sine functions. Every part of the wave oscillates as sin(ωt), but the amplitude of this oscillation depends on position x, with Asin(kx) acting as a position-dependent amplitude. So if one happens to be at a position where sin(kx)=0, for example at x=0, the amplitude of oscillation will be zero forever. Places where the amplitude is always zero are called nodes. Another way to think of this is to start with the function Asin(kx) and look what happens to it at different times when we multiply it by sin(ωt). At t=0, sin(ω0)=0 and the product is zero everywhere. At a slightly later time, we multiply sin(kx) by a nonzero number and the wave begins to emerge. So basically, the wave always looks like a stationary function sin(kx) that is simply scaled at different times by sin(ωt).

Use the above simulation to answer the questions in the pop-up window quiz.