What is light?
In our discussions up to this point, we talked about waves traveling in and being carried by a material. After all, you need something to disturb and a material which responds to that disturbance in order to carry that disturbance in a wave! Light, on the other hand, does not need a material in which to travel and in fact can travel in perfectly empty space (vacuum)! How can nothing carry something?!
The key to understanding light is to realize that it actually is composed of two waves, and electric and magnetic wave, and therefore is commonly referred to as an electro-magnetic wave. The electric and magnetic waves are coupled to each other. We will not go into rigorous details, as you may have already seen in Ampere's and Faraday's laws, changes in space and/or time of electric fields produce changes in time and/or space in magnetic fields, and vice versa. So at a given position in an electromagnetic wave, the changes in the electric field at that point produce changes in magnetic field at that position, which in turn again drive changes in the electric field. In this way, one can imagine that the electric and magnetic fields push and pull each other along to form a traveling wave. The simulation below shows how the electric and magnetic field waves travel together as light. Note that the electric field (E) and magnetic field (B) are always perpendicular to each other and are in phase (both are maximum at the same times/positions).
The strength and propagation direction of electromagnetic radiation is given by the Poynting vector, S. The magnitude of the Poynting vector represents the energy flux of the wave, or the power that the wave delivers per unit area perpendicular to the wave's travel direction. As can be seen in the equation below, for light traveling in vacuum, the Poynting vector at a given time and position is proportional to the cross product of the electric and magnetic fields composing the light wave at that same time and position:
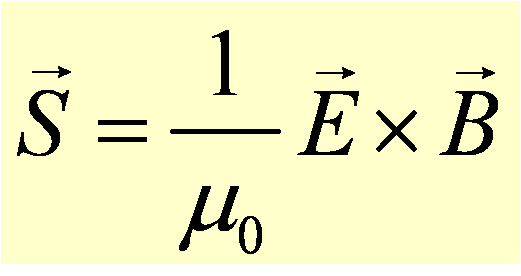
where μ0 is the permeability of free space (vacuum). It is interesting to note that although E and B change sign, their
cross product always points in the same direction. Look at the simulation above and check the cross product of E and B at different times
and places along the wave. Verify that the Poynting vector always points along the the direction in which the wave is traveling (the
z-direction in this case).
Use the above simulation to answer the following questions?

