Wave-Wave Interactions: Fourier Analysis: Periodic Functions

  In the next two pages we will look into how various sine waves can be added to create a wave. We will see that adding sine functions to produce a wave is analogous to adding vector components to produce a vector. We will learn how to determine the magnitude of each Fourier component. In the first page, we will begin with periodic functions, where the Fourier components have discrete frequencies that match the base periodicity of the periodic function. In the second page, we will look at non-periodic functions, where Fourier components can have a continuous range of frequencies. A interactive graphical simulation found at the bottom of each page can be used to visualize the basic ideas needed to get a conceptual grasp of Fourier analysis.

  A vector is made up of separate components that add up to form it. For example a three dimensional spatial vector used to describe the position of an object has x, y and z components. The x-component tells us how much of the vector lies in the x-direction, the y-component tells us how much of the vector lies in the y-direction, and the z-component tells us how much of the vector lies in the z-direction. This can be seen in the figure below:

  with A_x, A_z, and A_z weighting the unit vectors in the x, y, and z directions, respectively.

  In general, a vector can have an arbitrary number of dimensions and is given by:

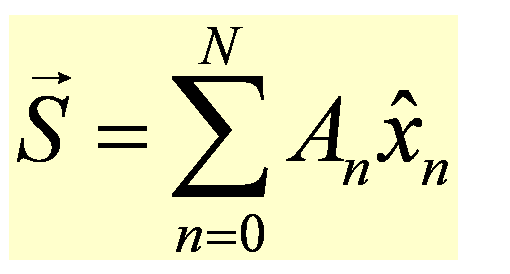
  The components that make up a vector are called a basis. In the case of three-dimensional position vectors, the basis consists of the three unit vectors in the x, y, and z directions. Any position vector can be represented as a weighted sum of these three unit vectors.

  We typically choose to represent vectors using orthogonal components, which means that each component represents a unique direction/dimension that cannot be produced by any combination of other components:

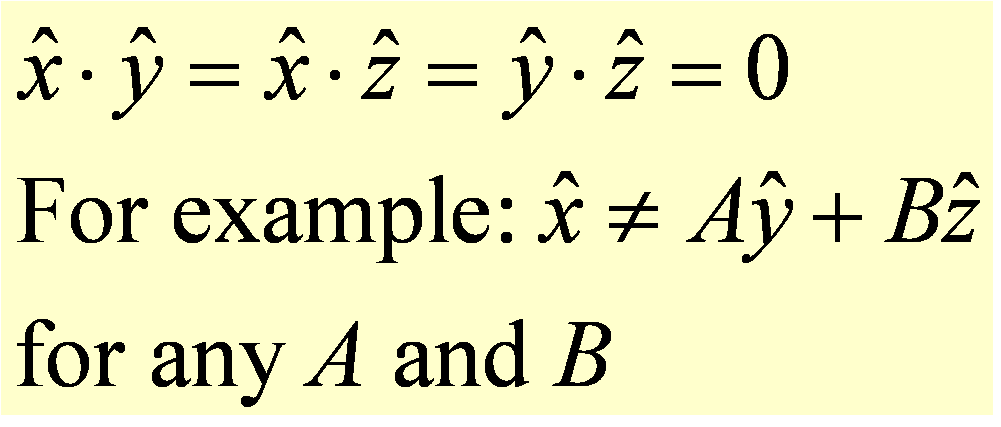
  The fact that the dot product of two orthogonal components is zero means simply that no part of one component lies in the direction of the other component. For example, in Cartesian coordinates, no combination of unit vectors in the y and z directions will be able to replace the unit vector in the x-direction, and one needs all three unit vectors to represent a three dimensional vector.

  We can use the othogonality of the unit direction vectors to determine how much a vector lies in a particular direction, by simply taking the dot product of the vector with the unit vector in that direction. For example, if we want to know how much of a vector lies in the x-direction, we take the dot product of that vector with the unit vector in the x-direction as shown below:

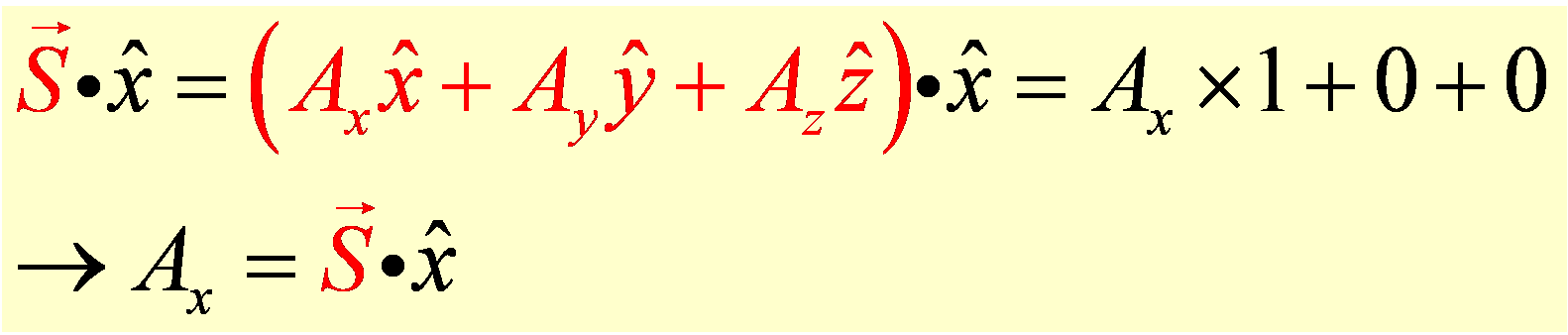
  Since the dot product of unit vectors that are not in the same direction is zero, the only term that survives on the right hand side of the equation above is A_x, which tells us how much of the vector lies in the x-direction and is exactly what we wanted to find.

  Just as two orthogonal linear (or left and right circular) polarization waves can be added to obtain any polarization state, sinusoidal functions can be added to produce any well-behaved mathematical function. By adding a series of sines, each with a distinct amplitude, frequency, and phase, one can produce virtually any mathematical function S(t), even functions that are not periodic. This has many important applications. For example, by controlling the amplitude, frequency, and phase of the sines that one adds, one can produce any waveform, which can then be sent to speakers to produce complex sounds.

  One can think of each frequency component in a function in the same way as different dimensions/directions in a vector. This is shown in the cartoon below:

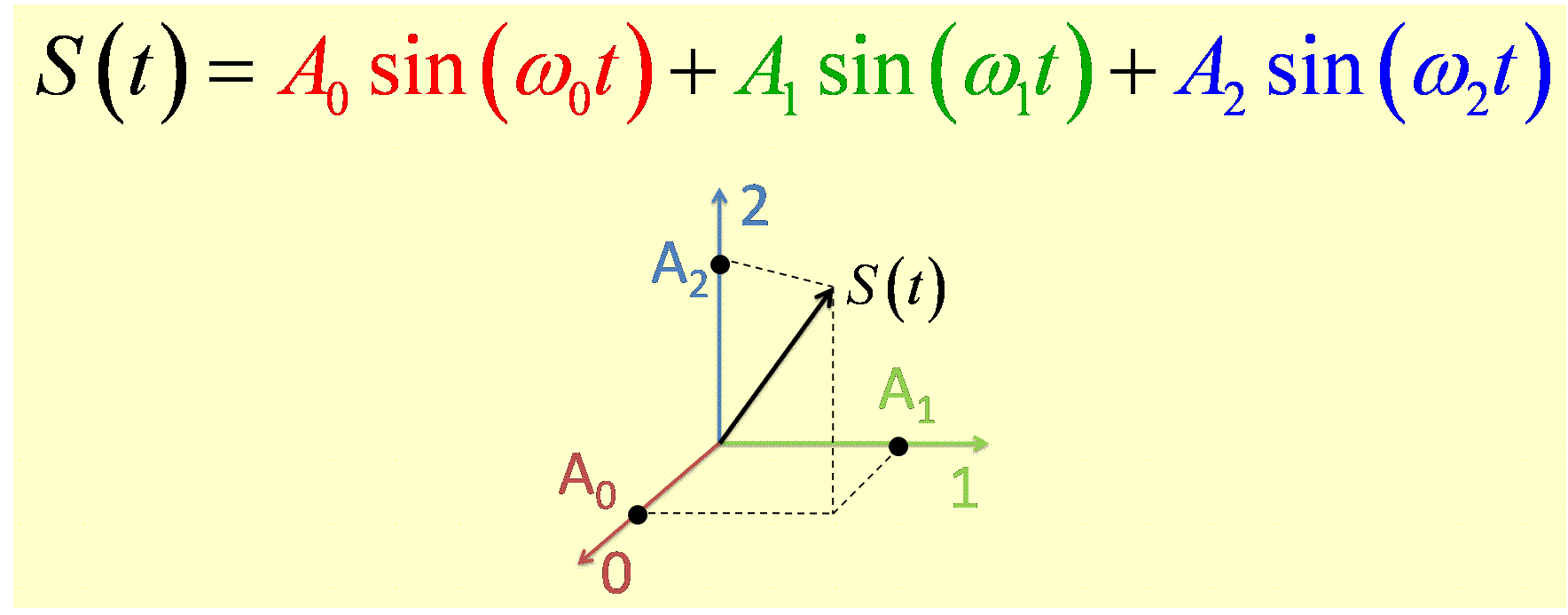
  Here the amplitudes A₀, A₁, and A₂ indicate the amplitudes of the sine waves at frequencies ω₀, ω₁, and ω₂, respectively, which add up to form S(t).

  We will show that these frequency components are orthogonal using a mathematical operation that is analogous with the dot product for vectors, but first let's start with a function S(t) that is periodic, with a period τ. Since S(t) returns to the same value after time τ, all the frequency components making up S(t) must also return to the same value after time τ. Note that we have chosen to deal with a function of time, but S could be a function of position or any other variable. Since the frequency components are orthogonal, if one of them did not return to the same value after time τ, it would be impossible in general to use the other components to fix this and therefore all the components must repeat after time τ. Note that these components may have significantly shorter periods than τ, but that in each case their periods go into τ an integer number of times, and hence the components also repeat with period τ. As a result, S(t) can be represented by a discrete series of sine functions with non-continuous frequencies ω_n=n×2 π/τ, where n is an integer from 0 to infinity. This discrete Fourier representation of a periodic function is shown below.

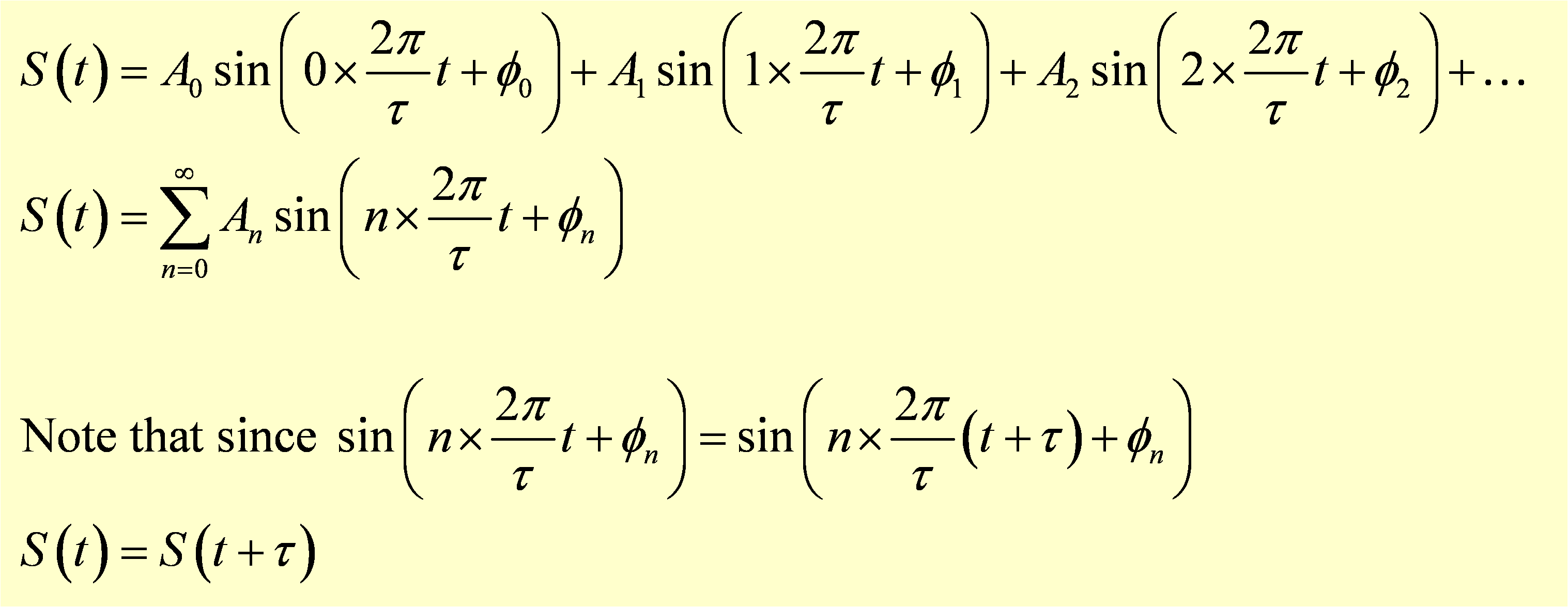
  The sine functions that add together to form the overall function are called Fourier components, and like vector components in a multidimensional vector they are orthogonal, meaning that no combination of Fourier components can be used to replace another component. Note that each Fourier component has an amplitude and a phase in addition to its frequency. The phase allows the component to be shifted in time, for example the component at a given frequency may look more like a cosine than a sign, with a maximum at t=0. Here we will not be too concerned with the phase of the components and in the simulation at the bottom of the page we will deal only with sine functions, i.e., functions that are 0 at t=0, to keep things simple.

  With vectors we used the dot product to check orthogonality of two components. In this case we multiply the two Fourier components and average them over time by integrating the product to see how much one component "overlaps" the other. This can be seen below:

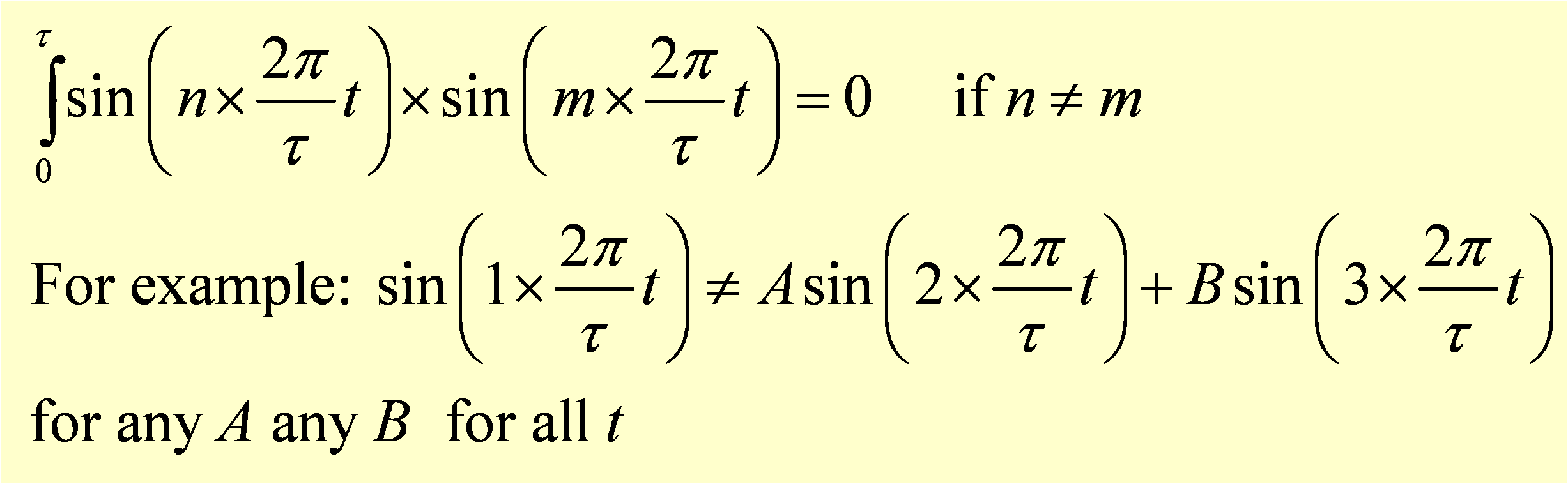
  Unless the frequencies of the two components are the same, the integral of the product of the component functions is exactly zero. If the two sine functions have the same frequency and phase, the average of the product can be normalized to 1, as shown below:

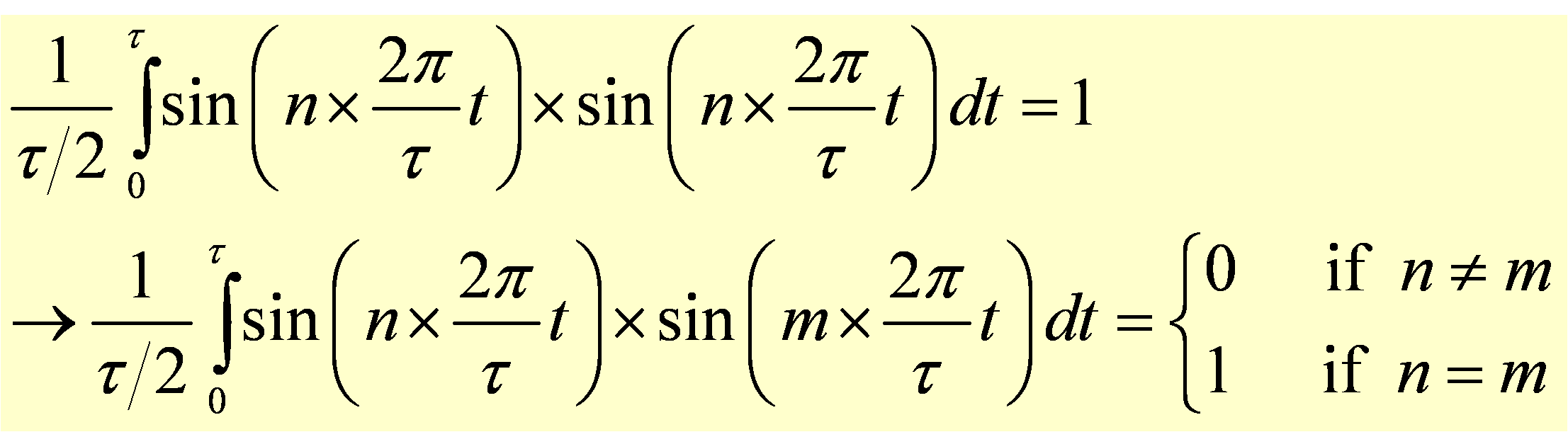
  We can build a signal by adding sine waves, but we can also do the inverse by taking a signal consisting of a complicated waveform (such as a sound wave) and breaking it up into its Fourier components to allow quantitative analysis and manipulation of the signal. This is especially useful when a signal at a known frequency is buried in a wave containing strong noise at other frequencies. Using Fourier analysis one can pick out the desired signal by measuring the component that is at the signal frequency. This projection is analogous to how one determines the x-component of a vector by taking the dot product of the vector with the unit vector in the x direction, as was shown earlier on this page. For example, to determine the magnitude of the sinewave component at frequency ω_m=m×2 π/τ contained in a function S(t), one simply multiplies the function by sin(ω_mt) and integrates over one period τ. Due to orthogonality, the components in the series making up S(t) that are not at frequency ω_m will vanish when multiplied by sin(ω_mt) and integrated over one period. The only term in the sum that will remain is the part of S(t) that is exactly at frequency ω_m. In this way we can determine the magnitude A_m of the component at frequency ω_m that contributes to S(t).

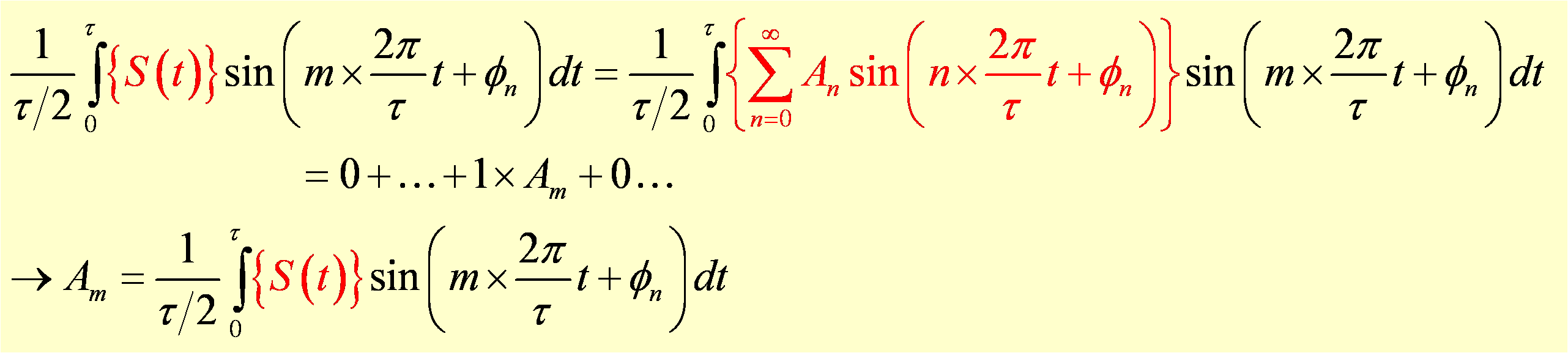
  Below is a Fourier analysis java applet that lets you find sinusoidal wave components in a periodic function. Notice that at certain Reference frequencies, the peaks and dips of the Reference wave line up with peaks and dips in the Signal function. When this happens, the product tends to be positive, with positive peaks multiplying positive peaks, and negative dips multiplying negative dips. If the frequencies are not the same, we get bot positive (positive peaks multiplying positive peaks and and negative dips multiplying negative dips) and negative (positive peaks multiplying negative dips and and negative dips multiplying positive peaks) contributions to the product. As a result, the product averages to zero if the Reference signal frequency does not match a frequency component in the Signal function.

  Although this is reminiscent of wave interference, where waves are added, we are actually MULTIPLYING waves here!

• Press "Load Curve" button to load the signal function.
• Slowly move "Reference Frequency" slider over its full range to select different reference functions.
• Observe how the Signal*Reference product averages to zero unless the Reference frequency is the same as one of the components in the Signal.
• Check the alignment of dips and peaks in the Signal and Reference functions; Check the (Signal)x(Reference) product panel; Check the Product Average window, which shows the integrated average of the (Signal)x(Reference) product.
• Set the Reference frequency to a position where the Product Average is a maximum and move the phase slider to change the phase of the Reference function with respect to the Signal. What happens when they are 90 degrees out of phase? What happens when they are 180 degrees out of phase?